

Suppose you want to build a ramp for access to a loading dock that is 4 feet above ground level. You want to be able to easily push a cart on wheels up the ramp, and the angle of elevation should be no more than 20\(^\). How long does the ramp have to be?
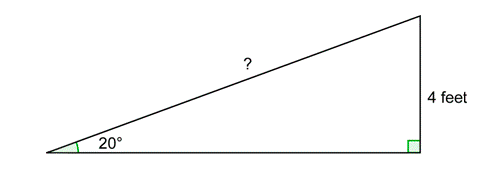
In this diagram, you have a right triangle for which you know the length of one side and the measure of an acute angle. You want to find the length of the hypotenuse. You may know that the Pythagorean Theorem enables you to find the length of one side of a right triangle, given the lengths of the other two sides. Now you will learn trigonometry, which is a branch of mathematics that studies the relationship between angles and the sides of triangles. In fact, trigonometry will allow you to find unknown side lengths and angle measures in right triangles in a variety of cases, such as in the problem above.
In the example above, one of the acute angles has a measure of 20\(^\). You could describe the side (or leg of the right triangle) with length 4 feet as the height of the triangle, or you could say that it is “opposite” the 20\(^\) angle. The other leg is said to be “adjacent” to the 20\(^\) angle. In trigonometry, this type of relationship between sides and angles is very important.
The general relationship between sides and angles is shown in the diagram below.
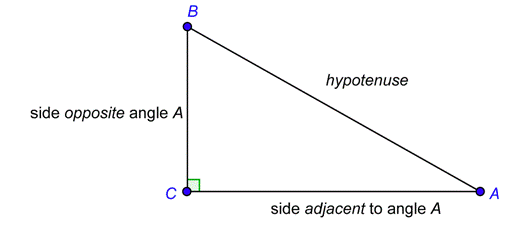
Angle \(A\) is formed by the hypotenuse and leg \(\overline\). We say that leg \(\overline\)is the side adjacent to angle \(A\). We say that leg \(\overline\) is the side opposite angle \(A\). In other words, the adjacent side is the leg that is part of the angle; the opposite side is the leg that is not part of the angle.
Problem: What is the length of the side opposite angle \(X\) and the length of the side adjacent to angle \(X\)?
Answer
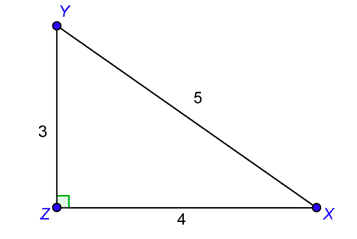
The side opposite angle \(X\) is \(\overline\). Its length is 3. The side adjacent to angle \(X\) is \(\overline\). Its length is 4.
opposite side length: 3
adjacent side length: 4
Keep in mind that the labels “opposite” and “adjacent” depend on which angle you are talking about. The side opposite an angle does not need to be the height of the triangle. Consider the following example:
Problem: What is the name of the side opposite the 40\(^\) angle and the name of the side adjacent to the 40\(^\) angle?
Answer
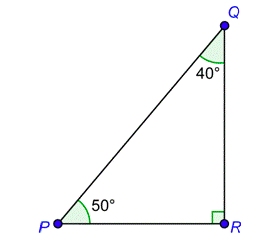
The 40\(^\) angle is formed by the hypotenuse and \(\overline\), so \(\overline\) is the adjacent side. Since \(\overline\) is not a part of the 40\(^\) angle, it is the opposite side.
opposite side: \(\overline\)
adjacent side: \(\overline\)
Each leg in a right triangle is adjacent to one of the acute angles and opposite the other acute angle.
Problem: In \(\bigtriangleup AB\), side \(\overline\) is adjacent to which angle and opposite which angle?
Answer
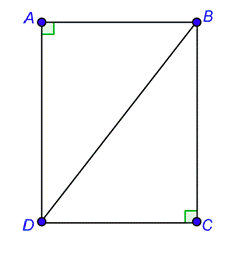
Side \(\overline\) and the hypotenuse \(\overline\) together form \(\angle ADB\). So \(\overline\) is adjacent to \(\angle ADB\). Since \(\overline\) is not part of acute angle \(\angle ABD\), \(\overline\) is the side opposite \(\angle ABD\).
adjacent to \(\angle ADB\)
opposite \(\angle ABD\)
Suppose your professor asks you and another student to draw a triangle with angle measures 35\(^\), 55\(^\), and 90\(^\). You and your friend will probably draw triangles of different sizes. However, because the triangles will have the same angle measures, they will be similar.
Remember that this means that the triangles will have proportional corresponding sides. For example, one triangle might have sides that are all twice as long as the sides of the other, as seen below.
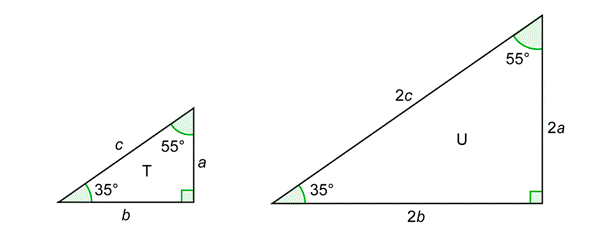
Now suppose that each of you has been asked to find the ratio of the side opposite the 35\(^\) angle over the hypotenuse. Even though you are using different triangles and will have different numbers in the numerator and denominator, you will still end up with the same result. The two of you will get:
The two ratios are the same because the 2s cancel. If you draw a triangle with the same angles and sides that are three times as long as those of triangle T, the ratio of the side opposite 35\(^\) over the hypotenuse will be \(\frac = \frac\). This ratio will be the same for all similar triangles, and this ratio is called the sine of 35\(^\). Sine is abbreviated as \(\sin <35^>\).
The same type of result will happen if you use other ratios of sides. For example, if you take the ratio of the side adjacent to 35\(^\) over the hypotenuse, you will get \(\frac\) no matter which of the above triangles you use.
In addition to the sine ratio, there are five other ratios that you can compute: cos, tan, cot, sec, and csc. Just as sin is an abbreviation for sine, cos is short for cosine, tan is short for tangent, csc is short for cosecant, sec is short for secant, and cot is short for cotangent. (When reading these abbreviations aloud, you need to say the complete word.) These six ratios will help you find unknown side lengths and unknown angle measures in right triangles. Let’s look at definitions for these six ratios, starting with a typical right triangle like the one below.
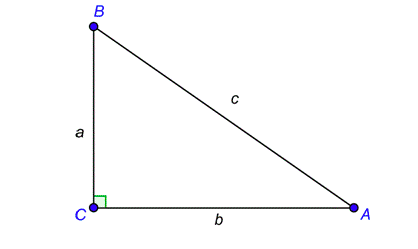
The definitions are as follows:
Given these definitions, let’s practice applying them.
Problem: Determine the six trigonometric ratios for angle \(D\) in the right triangle below.
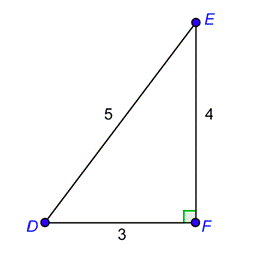
The first thing you need to do is recognize that \(\overline\) is opposite angle \(D\) and \(\overline\) is adjacent to angle \(D\). Then write down their lengths.
length of side opposite \(D\) = 4
length of side adjacent to \(D\) = 3
length of hypotenuse = 5
Substitute these values into the definitions for the six ratios.
Notice that the values of sine and cosine are between 0 and 1. You found them by dividing the length of a leg by the hypotenuse. The hypotenuse is the longest side, so the numerator is less than the denominator. That means the output of the sine or cosine function is always less than 1.
Keep in mind that the opposite side for one acute angle is the adjacent side of the other acute angle. In the example above, side \(EF\) was the opposite side for angle \(D\). But, as you’ll see in the next example, it will be the adjacent side for angle \(E\).
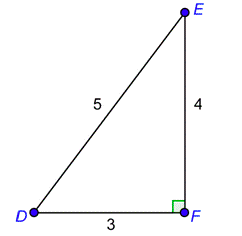
Problem: Determine the six trigonometric ratios for angle in the right triangle below.
Answer
This is the same triangle that you saw in the previous example, so the hypotenuse is the same. The difference is that you are looking at the triangle from the perspective of angle \(E\) instead of angle \(D\). So the opposite and adjacent sides switch places. That is, \(\overline\) is adjacent to angle \(E\) and \(\overline\) is opposite to angle \(E\).
length of side opposite \(E\) = 3
length of side adjacent to \(E\) = 4
length of hypotenuse = 5
Substitute the new values into the definitions for the six ratios.
If you compare the answers to the last two examples, you will see the following:
\(\sin D = \frac = \cos E\)
These two trigonometric functions are equal because the opposite side to angle \(D\) (which is 4) is the adjacent side to angle \(E\). Because they are the two acute angles in a right triangle, \(D\) and \(E\) are complementary. That is:
Substitute this into the equation above:
Again, the reason these two functions are equal is that the opposite side to one acute angle is the adjacent side to the other acute angle. This is true in any right triangle. So if \(A\) is any acute angle, it is always true that:
Comparing more answers from the last two examples, you can find these relationships:
\(\sec D = \frac = \csc E and \tan D = \frac = \cot E\)
You get these equalities because (1) the adjacent side to angle \(D\) is 3, while this is the opposite side to angle \(E\), and (2) the opposite side to angle \(D\) is 4, while this is the adjacent side to angle \(E\). These are examples of the general relationship we have stated: the opposite side to one acute angle is the adjacent side to the other acute angle. Using the same reasoning as above, if \(A\) is any acute angle, it is always true that:
An equation, such as any of the three above, that is true for any value of the variable is called an identity. Note the full names of these functions: sine and cosine, secant and cosecant, tangent and cotangent. These pairs are referred to as cofunctions. The angles \(A\) and \(90^ - A\) are complementary. In other words, the cofunctions of any pair of complementary angles are equal.
You can use these relationships to find values of trigonometric functions from values of other functions without drawing a triangle. Note that you can replace \(A\) and \(90^ - A\) by \(B\) and \(90^ - B\). The different letter will not change the relationship, because these angles are still complementary.
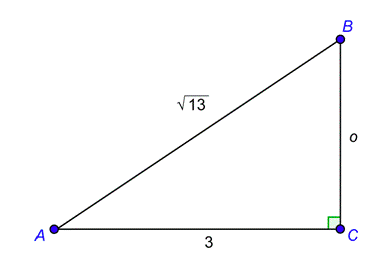
Problem: A right triangle has acute angles \(A\) and \(B\). If \(\sin A = \frac\) and \(\tan B = \frac\), what are \(\cos B\) and \(\cot A\)?
Since \(A\) and \(B\) are the acute angles in a right triangle, they are complementary angles.
Substitute for \(B\). Use the identity (the cofunctions are equal). Substitute the given value.
Substitute for \(A\). The cofunctions of any pair of complementary angles are equal. Substitute the given value.
\(\cos B = \frac , \cot A = \frac
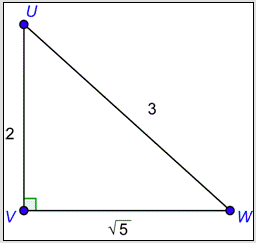
What are the values of \(\cos U\) and \(\csc U\)?
The six ratios or functions are usually thought of as two groups of three functions. The first group is:
One way to remember these three definitions is with a memory device that uses the first letter of each word. The definition of sine is represented by soh (sine equals opposite over hypotenuse). Likewise, the definition of cosine is represented by cah (cosine equals adjacent over hypotenuse), and the definition of tangent is represented by toa (tangent equals opposite over adjacent). Putting these together gives you sohcahtoa.
The second group is:
If you compare these three ratios to the three above them, you’ll see that these three fractions are the reciprocals of the three fractions above them. That is, cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent. Writing this gives three more identities:
| \(\csc A=\frac\) | \(\sec A=\frac\) | \(\cot A=\frac\) |
|---|
If you remember sohcahtoa plus these three identities, you can find the values of any trigonometric functions, as seen in the following example.
Problem: For acute angle \(A\), \(\sin A = \frac\) and \(\cos A = \frac\). Find the values of the other four trigonometric ratios for angle \(A\).
Answer

The definition of sine tells you that \(\sin A = \frac = \frac\). A triangle with o = 7 and h = 25 will have this ratio.
You also know that \(\cos A = \frac = \frac\). You are given \(\cos A = \frac\), so \(a = 24>\).
Now you have all three sides of the triangle and you can use the definition of tangent.
Next, use the three reciprocal identities to obtain the other three ratios.
The value of any trigonometric function is a ratio, or a fraction. Remember that fractions can be reduced.
Problem: For acute angle \(A\), \(\cos A=\frac>\) and \(\tan A=\frac\). Find the values of \(\sin A\) and \(\csc A\).
Answer
You want a right triangle where the ratio of the side adjacent to angle \(A\) over the hypotenuse is \(\frac>\). A triangle with sides \(a = 3\) and \(h = \sqrt\) would have this ratio.
You can use the definition of tangent to find the opposite side. Substitute the value you are given for tangent and then solve the equation.
Now you have all three sides. Use the definition of sine to find its value.
Now using the reciprocal identity, the \(\csc\) can be found by taking the reciprocal of the \(\sin\).
Remember that the sides of a right triangle satisfy the Pythagorean Theorem. So if \(a\) and \(b\) are the lengths of the legs, and \(c\) is the hypotenuse, you must have \(a^2 + b^2 = c^2\). In the last example, the lengths of the legs were 2 and 3, and the hypotenuse was \(\sqrt\), and it is true that \(2^2 + 3^2 = \sqrt^2\).
Which of the following could be the values of the trigonometric functions of the same angle?
You know that if you draw similar triangles with angle measures \(35^\), \(55^\),and \(90^\), the ratio of the side opposite \(35^\) to the hypotenuse will be the same for all those triangles. This is \(\sin 35^\). The easiest way to find what this ratio actually equals is with a scientific or graphing calculator.
Looking at a calculator, you will find a key that says SIN on it. You can use this to find the value of \(\sin 35^\). Keep this in mind: you need to know that there are different units for measuring angles. For our purposes, make sure that your calculator is set in the “degree mode.” (The following instructions are generalized, but you may need to refer to your calculator’s instruction manual for how to perform these calculations on your particular calculator.)
If you use a scientific calculator, look in the display and see if it says DEG in small letters above the 0 (as opposed to RAD or GRAD). If it does not, press the DRG key until the display says DEG. Now enter 35, and then press the SIN key. The result is \(\sin 35^\):
If you have a graphing calculator, press the MODE key. The third line of the display will say RADIAN DEGREE. Use the arrows to select DEGREE, then press ENTER, 2ND, QUIT. Now the calculator is in degree mode. On a graphing calculator, you enter things the same way as you would write them. So press the keys to give you \(\sin (35)\) on the display and then press ENTER. You should now see the value on the next line of the display.
Because sine is a function, given an angle measure \(X\) (the input), your calculator will give you the value of \(\sin X\) (the output). All the right triangles with acute angle measure \(X\) will be similar, so the ratio of the opposite side to the hypotenuse will be the same for all of those triangles. Therefore, the ratio depends only on the value of \(X\); it does not depend on the triangle.
Likewise, the other five trigonometric ratios are functions. You can use your calculator to find the value of those functions. You will notice that next to the SIN key there are COS and TAN keys, which can be used to find the values of cosine and tangent.
Problem: Use your calculator to find the values of \(\cos 35^\) and \(\tan 35^\) to the nearest thousandth.
Answer
On a scientific calculator, enter 35, then press COS. Do this in the reverse order for a graphing calculator.
Remember to look at the ten thousandths place to help you round to the nearest thousandth.
Use the same procedure for tangent.
\(\cos 35^ \approx 0.819 \text < and >\tan 35^ \approx 0.700\)
You may have noticed that your calculator has no keys for \(\csc\), \(\sec\), or \(\cot\). You can still use it to find the values of these functions. You can do this by using the calculator in combination with the reciprocal identities. You must first find the value of \(\sin\), \(\cos\), or \(\tan\), and then find the reciprocal, as this next example shows.
Problem: Use your calculator to find the values of \(\csc 50^\), \(\sec 50^\), and \(\cot 50^\) to the nearest thousandth.
Answer
First use your calculator to find the value of \(\sin 50^\). Do not round this value until you are writing the final answer.
Press the key that says \(\frac\) or \(x^\). This will give you the value of cosecant.
Now round your final answer to the nearest thousandth.
Find the value of \(\cos 50^\). Then find the reciprocal and round off.
Find the value of \(\tan 50^\). Then find the reciprocal and round off.
\(\csc 50^ \approx 1.305, \sec 50^ \approx 1.556, \text < and >\cot 50^ \approx 0.839\)
What is the value of \(\csc 17^\) to the nearest thousandth?
So far you have learned the definitions of the six trigonometric functions. Remember that a function has an input and an output. For each of these functions, the input is the angle measure and the output equals a certain ratio of sides. Your calculator can be used to find the values of these functions. For example, if the angle measures \(60^\), the cosine of the angle is 0.5. This can be represented as \(\cos 60^=0.5\).
Now what if the situation were reversed? What if you knew the value of the ratio and wanted to know the angle that produced it? That is, what if you knew the output of a trigonometric function, and wanted to know the input? For example, you might know that the cosine of some angle is 0.5 and want to find out what the angle is. You can use your calculator to find these values, too.
In general, when you reverse the input and the output of a function, what you get is called an inverse function. Your calculator can find the inverses of sine, cosine, and tangent. In the example above, on a scientific calculator you would enter 0.5, press the 2ND key, then press COS. The display would show 60. (Make sure that your calculator is set on degrees!) This tells you that the angle is \(60^\). On a graphing calculator, you would press 2ND, then COS, then 0.5, and finally ENTER. (Keep in mind that you may need to refer to your calculator’s instruction manual for how to perform these calculations on your particular calculator.)
Above the SIN, COS, and TAN keys you will see \(\sin ^, \cos ^\) and \(\tan ^\). These are the inverse trigonometric functions, and the way to read them out loud is: arcsine, arccosine, and arctangent. The result mentioned above can be written as \(\cos ^ 0.5=60^\) or \(\arccos 0.5=60^\).
If you were given the value of the sine (or tangent) function and wanted to know what angle produced it, you would follow a procedure similar to that described above. So on a scientific calculator, you would enter the value, press the 2ND key, then press SIN (or TAN).
Problem: Use your calculator to find the angle, to the nearest degree, whose tangent value is 0.75.
Answer
On a scientific calculator, enter 0.75, then press the 2ND key and TAN. Do this in the reverse order for a graphing calculator.
Look at the tenths place to help you round to the nearest degree.
If you are given the expression \(\cos ^ 0.24\), for example, you can interpret this as saying, “Find the angle whose cosine equals 0.24.”
Problem: Determine \(\cos ^ 0.24\) to the nearest tenth of a degree.
Answer
On a scientific calculator, enter 0.24, then press the 2ND key and COS. Do this in the reverse order for a graphing calculator.
Look at the hundredths place to help you round to the nearest tenth.
Remember that this means \(\cos 76.1^ \approx 0.24\).
Here is a real-world example using an inverse function.
Problem: A skateboard ramp is 7 feet long with one end on the ground and the other end 2 feet above the ground. What is the angle of elevation to the nearest tenth of a degree?
Answer
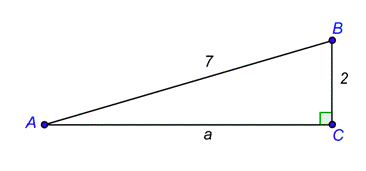
The angle of elevation is angle \(A\). Because you know the opposite side and the hypotenuse, you can use the sine function.
Use the definition of sine. The unknown is the input.
You can rewrite this equation using arcsine. You need to reverse the input and the output.
On a scientific calculator, divide 2 by 7, then press the 2ND key and SIN. Do this in the reverse order for a graphing calculator.
Remember that the sine or cosine function cannot have an output greater than 1. With arcsine and arccosine, you are reversing inputs and outputs. Consequently, the input of these functions cannot be a number bigger than 1. If you try to compute \(\sin ^ 2\) with your calculator, for example, you will get an error message.
If \(\sin x = \frac\), what is \(x\) to the nearest hundredth of a degree?
The six trigonometric functions are defined as ratios of sides in a right triangle. Their values depend only on the angle and not on any particular right triangle. A good way to remember the definitions of sine, cosine, and tangent is with the memory device sohcahtoa. The other three functions, cosecant, secant, and cotangent, are reciprocals of the first three.
You can use a calculator to find the values of these functions or ratios. You can also use a calculator to find the values of the inverse trigonometric functions. That is, given the ratio, you can find the angle that produced it.
This page titled 19.1.1: Identifying the Six Trigonometric Functions is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by The NROC Project via source content that was edited to the style and standards of the LibreTexts platform.